CPU Scheduling Algorithm Analysis
This analysis of CPU scheduling algorithms covered the algorithms commonly referred to as First Come
First Served (FCFS), Shortest Job First (SJF), Shortest Job Remaining (SJR), Round Robin (RR) and Priority (Pr).
These names tend to be very descriptive of the actual algorithm involved. In FCFS, the first process to arrive in the
ready queue is the first to be executed, and it executes until it is no longer ready. Shortest Job First takes that
shortest job in the queue, executes it, and then re-evaluates all the processes in the queue and again takes the shortest
job. Shortest Job Remaining re-evaluates the ready queue every time a process arrives in the queue, always taking
the process with the shortest remaining execution time. Round Robin takes processes in a FCFS manner, but only
lets them execute for a time period known as a quantum. If the process has not finished during this quantum, the
process is pre-empted and placed on the end of the ready queue. The priority functions in a manner similar to the
SJR algorithm. It evaluates each process and takes the process with the highest priority to execute first. Every time
a new process arrives in the ready queue, this choice is re-evaluated, possibly taking a different process after the
preemption.
These algorithms were implemented in a C program, utilizing a few features of C++ (the new operator
mainly). Statistics were generated, such as average wait time for all processes in one simulation, and over 10
simulations of the same algorithm. This data has been compiled into the following table. 10 simulations were
performed on each of these trials:
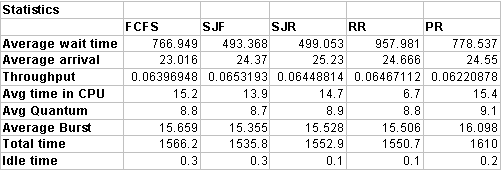 Average wait time is defined by the sum for all processes of the last time a process got the CPU, minus it's
previous time in CPU, minus its arrival time, all divided by the number of processes. Average arrival is a simple
mean of the arrival times of all the processes. Average Throughput is number of processes over time. I chose this to
be number of processes over Time. (Time is the total time the processor spent executing a selection of processes).
The average time in CPU is calculated by the totalburst time of all processes divided by the number of intervals on
the Gantt chart. This is calculated in my algorithm as intervals and is incremented every time a change in process
occurs. The average quantum is calculated base on 60% of the average burst. On that note, average burst is
totalburst (defined above) over number or processes. Total time is the total time it took to execute all these
processes, including any idle time waiting for a new process to be ready. Typically, idle time only occurred at the
beginning of an execution, when no processes arrived at time 0, and in one case time 1. See the attached detailed
Excel tables for statistics on each simulation run.
Average wait time is defined by the sum for all processes of the last time a process got the CPU, minus it's
previous time in CPU, minus its arrival time, all divided by the number of processes. Average arrival is a simple
mean of the arrival times of all the processes. Average Throughput is number of processes over time. I chose this to
be number of processes over Time. (Time is the total time the processor spent executing a selection of processes).
The average time in CPU is calculated by the totalburst time of all processes divided by the number of intervals on
the Gantt chart. This is calculated in my algorithm as intervals and is incremented every time a change in process
occurs. The average quantum is calculated base on 60% of the average burst. On that note, average burst is
totalburst (defined above) over number or processes. Total time is the total time it took to execute all these
processes, including any idle time waiting for a new process to be ready. Typically, idle time only occurred at the
beginning of an execution, when no processes arrived at time 0, and in one case time 1. See the attached detailed
Excel tables for statistics on each simulation run.
These results imply that both Shortest Job First and Shortest Job Remaining perform similarly when the
burst time can be predicted, and both perform much better than other scheduling types, in terms of average wait
time. Round Robin has by far the worst average wait time, and a considerably smaller average quantum than the
other methods. This quantum greatly delays the finishing of any process. Priority seems to work about the same as
First Come First Served, but this is probably due to the low number of available priority levels available in this
system. Shortest Job First and Shorts Job Remaining function very similarly to Priority scheduling, except for the
method in assigning the priorities. By limiting the number of randomly assigned priorities to 5, Priority scheduling
tended to drop down into a First Come First Served scheduling for elements of the same priority, of which
approximately 20 of each priority should exist. This in turn means that priority will tend to act like First Come First
Serve, though with a higher average wait time (due to processes with lower priorities waiting a long time to begin
execution). With a greater number of available priorities, performance should improve somewhat, probably to
something between First Come First Served and Shortest Job Remaining or Shortest Job First. These results would
seem to indicate that in predictable situations where a low average wait time is desired, Shortest Job First and
Shortest Job Remaining are ideal choices. First Come First Served is good when simplicity is desired, and Priority
can probably be used well in less predictable situations where slightly better average wait times are desired. Round
Robin is best used when many processes need to be run, and all should get some processor time consistently, and
when average wait time does not have to be very low.
The C code I used utilized Borland's randomize() and rand() to generate random numbers. Borland claims
to have a period of 232 in this function. I was able to detect no consistent patterns in data from the many trials I ran
of this program
This program is basically split into three main parts: a user interface, a scheduling function, and a supporting
function. The only portion of this that is significant is the scheduling function. The user interface, contained in
main(), simply generates a set of parameters to pass on to schedule(). Schedule() in turn performs the entire
scheduling algorithm for all five algorithms, with only calls outside to I/O functions and a mergeSort function that
was used from the code currently being used n CSC 220.
Schedule functions in a traditional C design. Since we are dealing with random data, it can be generated
entirely in this scheduling function. I could've encapsulated this into a separate function, but many of the functions
in this are so small compared to the actual implementation of the algorithm, the extra effort seemed to be wasted. To
generate the data to later schedule, a simple for loop is used to generate N (one of the parameters) processes worth of
data into the array arrival. This name was chose due to its main purpose. This array holds (after a quick
mergeSort), all the processes that will be modeled, sorted by arrival time. This makes this array extremely useful, but
not to do perform any actual scheduling on. To actually model the scheduling of a process, a ready queue was
needed. This suggests a second array, ready, the same size as arrival. This array has elements copied into it based
on the variable time. Time represents the cpu counter, from the beginning of the simulation. As new elements arrive
(time is greater than their arrival time) they are copied from arrival into ready, with this line of code:
ready[procsincpu++]=arrival[arrivedprocs++];
Several things should be noted here. The first is that two separate counters into these arrays are used. This is due to
the simplicity of the line, and the fact that this allows me to do some error checking later in case one of these gets
changed. Most likely, one of these could be accidnetly changed due to an error in coding, but not both of them,
therefore the while loop that contains this code has the condition (procsincpu == arrivedprocs) as a boundary on its
execution.
After allowing new processes to arrive with the above code, the algorithm specific code begins. A simple
switch/case construct allows a specialized sort for each algorithm, and the variable curproc is set to point into ready
at the current process. This process must not have completed executing, unless no process that has not completed is
currently in the ready queue.
Following this switch, a generic handler is executed, with a few special tests for the Round Robin algorithm
This code detects the several possible cases that can exist and handles them, marking processes that finish executing
as complete and miscellaneous other statistical tasks.
Finally, new processes are allowed to arrive again. This is here to facilitate the next line of code, which sets
the current processes sequence number to the sequence counter. This allows the Round Robin algorithm to sort on
the sequence number of each process (which is incremented and assigned as they arrive in the ready queue), and get
the desired behavior of the Round Robin algorithm.
The last thing that happens in the while loop is a check for a problem condition. All modifications to time
happen in the generic process handling section mentioned above. If this code doesn't execute at time 0, because no
processes have arrived at time 0 (possible due to the random nature of the arrival time), an infinite loop can occur.
To counter this, time is incremented by one, and idletime is also incremented by one. This idletime is used to track
how much CPU time is wasted due to this random occurrence. The most I encountered was a 2 cycle delay in one of
the over 100 trials I ran with full statistics on.
After the while loop terminates, some statistics are generated, and output to the screen, while others are
dumped to a disk file.
The code I used follows here:
#include <iostream.h>
#include <fstream.h>
#include <stdlib.h>
// globally defined statistic file. (defined globally because I couldn't remember how to pass streams as parameters)
fstream outfile;
typedef struct
{
int pnum, atime, burst, priority, prevtimeincpu, tleft, laststarttime, done, seqnum;
}
processM;
/* processM is the generic process I used here. Pnum is the process number, used as a final arbiter of precedence in scheduling
atime is the arrival time
burst is the amount of time the process will execute for
priority is the priority used for the Priority scheduling algorithm
prevtimeincpu is the time this process has spent in the cpu during other times. It was preempted out of those, and has been selected to execute a
second time.
tleft is the time this process has remaining to execute. This is used primarily as a sorting device for shortest job remaining, and a tracking device for
all the algorithms
laststarttime is another statistical tool, used in conjunction with prevtimeincpu to calculate average wait time
seqnum is used for round robin scheduling to provide a hard ordering of the processes, and an easy way to move an active process off the queue
after processes that arrive during this processes execution.
*/
typedef enum
{
FCFS, SJF, SJR, RR, Pr
}
sched_type;
// sched_type is used primarily to select the scheduling type for use in Schedule.
typedef enum
{
pnum, atime, burst, priority, prevtimeincpue, laststarttime, done, tleft, seq
}
sfield;
// sfield is used to tell mergeSort which subfield of processM to sort on.
void schedule (int N, sched_type stype, int K, int P, int M);
// K is the max burst time
// P is lowest priority (highest number)
// M is max arrival time
// schedule implements the different scheduling algorithms
// N = number of processes
// stype tells it which algorithm to use
// fullstats toggles different displays of stats at termination (and storage to file of the entire process table)
void mergeSort (processM * Key, int low, int high, int size, sfield field);
// mergeSort() sorts from low to high, in an array of size size, using field as an indicator of the key to sort on
void main (void);
// handles user interface and repeated simulations
// calls schedule(...) according to user input.
// also opens any needed output files (process table storage mainly)
void schedule (int N, sched_type stype, int K, int P, int M)
{
processM *arrival, // arrival is the array for all process (generated) before moving them into ready
*ready; // ready is all cpus that have arrived in the cpu (time >= ready[n].atime)
int pendingprocs = 0, // how many processes are currently in the CPU and haven't finished executing
time = 0, // the current CPU counter
procsincpu = 0, // how many processes have arrived, and a pointer to the next unused element of ready[]
arrivedprocs = 0, // the same as procsincpu, but pointing to arrival[]
curproc = 0, // the current process (pointing into ready[]), selected by the switch statement below
oldtime = 0, // the same as time, but used as a comparison to make sure we don't loop endlessly with no processes to execute
i, // i are general for() loop control variables
totalburst = 0, // statistical value used to hold the sum of all bursts in all processes
Q = 0 , // the chosen quantum value (defined to be 0.60 of totalburst)
idletime = 0, // how much time was spent idling, waiting for processes to arrive
intervals = 0, // how many different processes were in the CPU. Also the intervals on the corresponding Gantt chart
oldpnum = 0, // the process number of the last process in the cpu, used to detect when a new process has reached the CPU
seqnum = 0, // the number of the next process to be added to the queue, usually to the end of it. Only used in Round Robin scheduling
maxinc = 0, // the maximum value the time can be incremented by
thistimeincpu = 0;
// how long the process pointed to by oldpnum has been executing in the cpu, used to adjust prevtimeincpu when the process terminates
float avgwait, avgatime;
// storage places for average wait time and average arrival time
fstream procfile;
// file to dump the fully calculated ready[] array when finished executing
cout <<endl<< "Opening " ;
switch(stype)
{
case(FCFS):procfile.open("fcfs.txt", ios::out); cout << "fcfs.txt";break;
case(SJF):procfile.open("sjf.txt",ios::out); cout << "sjf.txt"; break;
case(SJR):procfile.open("sjr.txt",ios::out);cout << "sjr.txt"; break;
case(RR):procfile.open("rr.txt",ios::out);cout << "rr.txt"; break;
case(Pr):procfile.open("pr.txt",ios::out);cout << "pr.txt"; break;
default:procfile.open("procs.txt",ios::out);cout<<"procs.txt";break;
}
cout<<endl;
// allocate storage for both major arrays.
arrival = new processM[N];
ready = new processM[N];
// generate the processes randomly, according to the parameters given above
for (i = 0; i < N; i++)
{
arrival[i].pnum = i;
arrival[i].atime = (rand () % (M + 1));
arrival[i].burst = (rand () % (K)) + 1;
arrival[i].tleft = arrival[i].burst;
arrival[i].priority = (rand () % (P)) + 1;
arrival[i].prevtimeincpu = 0;
arrival[i].laststarttime = 0;
arrival[i].done = 0;
};
// sort arrival[] based on arrival time
mergeSort (arrival, 0, N - 1, N, atime);
// calculate Q as 0.60 * average burst
totalburst = 0;
for (i = 0; i < N; i++)
totalburst += arrival[i].burst;
// calculation is organized this way to minimize rounding errors due to division
Q = ((6 * totalburst) / (N * 10));
// initialize all the variables that get used in the while loop
pendingprocs = 0;
time = 0;
procsincpu = 0;
arrivedprocs = 0;
curproc = 0;
oldtime = 0;
idletime = 0;
intervals = 0;
oldpnum = -1;
seqnum = 0;
thistimeincpu = 0;
// (arrivedprocs==procsincpu) is simply an error check, while the other half of the while condition contains the boundary conditions for the loop
while ((arrivedprocs == procsincpu) && ((arrivedprocs < N) || (pendingprocs > 0)))
{
// notice starting time of this iteration
oldtime = time;
// let new processes hit the queue
if (procsincpu < N)
{
while (arrivedprocs < N)
if (arrival[arrivedprocs].atime <= time)
{
ready[procsincpu++] = arrival[arrivedprocs++];
ready[procsincpu - 1].seqnum = seqnum++;
pendingprocs++;
}
else
break;
};
// guts of scheduling algorithms are here, each case sorts ready[] appropriately if it needs to be, and selects the next process to execute.
if(procsincpu>0)
switch (stype)
{
case (FCFS):
for(curproc=0;(curproc<procsincpu)&&(ready[curproc].done);curproc++);
break;
case (SJF):
mergeSort (ready, 0, procsincpu - 1, procsincpu, burst);
for(curproc=0;(curproc<procsincpu)&&(ready[curproc].done);curproc++);
break;
case (SJR):
mergeSort (ready, 0, procsincpu - 1, procsincpu, tleft);
for(curproc=0;(curproc<procsincpu)&&(ready[curproc].done);curproc++);
break;
case (RR):
mergeSort (ready, 0, procsincpu - 1, procsincpu, seq);
for(curproc=0;(curproc<procsincpu)&&(ready[curproc].done);curproc++);
break;
case (Pr):
mergeSort(ready,0,procsincpu -1,procsincpu,priority);
for(curproc=0;(curproc<procsincpu)&&(ready[curproc].done);curproc++);
break;
};
// this portion increments time and updates statistics for the currently executing process
if(curproc < procsincpu)
{
// set maxinc
if(arrivedprocs<N)
{
if(stype==RR) maxinc=Q;
else maxinc = arrival[arrivedprocs].atime-time;
if(maxinc>ready[curproc].tleft)
maxinc = ready[curproc].tleft;
}
else // no preemption possible
{
maxinc = ready[curproc].tleft;
if((maxinc>Q)&&(stype==RR))
maxinc=Q;
};
if(ready[curproc].pnum != oldpnum)
{ // the selection method has chosen a different process than last time, reset the statistical values
oldpnum = ready[curproc].pnum;
ready[curproc].laststarttime = time;
thistimeincpu = 0;
intervals++;
};
ready[curproc].tleft -= maxinc;
time += maxinc;
thistimeincpu+=maxinc;
ready[curproc].prevtimeincpu += maxinc;
if(ready[curproc].tleft == 0)
{
ready[curproc].prevtimeincpu -= thistimeincpu;
ready[curproc].done = 1;
pendingprocs--;
}
}
// make sure we don't loop endlessly due to idle processor
if (time == oldtime)
{
time++;
idletime++;
};
// let new processes hit the queue (placed here also for Round Robin)
if (procsincpu < N)
{
while (arrivedprocs < N)
if (arrival[arrivedprocs].atime <= time)
{
ready[procsincpu++] = arrival[arrivedprocs++];
ready[procsincpu - 1].seqnum = seqnum++;
pendingprocs++;
}
else
break;
};
// for Round Robin - move the active process to the end of the queue
ready[curproc].seqnum = seqnum++;
}; // end while()
// do statistics here.
mergeSort (ready, 0, N - 1, N, atime);
avgwait = 0;
avgatime = 0;
for (curproc = 0; curproc < N; curproc++)
{
avgwait += ready[curproc].laststarttime - ready[curproc].prevtimeincpu - ready[curproc].atime;
avgatime += ready[curproc].atime;
procfile << "Proc: " << ready[curproc].pnum << " Arrival: " << ready[curproc].atime << " Burst: " << ready[curproc].burst
<< " priority: " << ready[curproc].priority
<< " wait: " << (ready[curproc].laststarttime - ready[curproc].prevtimeincpu - ready[curproc].atime) << endl;
}
avgwait = avgwait / N;
avgatime = avgatime / N;
cout << " Average wait time = " << avgwait << endl;
cout << " Average arrival = " << avgatime << endl;
cout << " Throughput = " << float (N) / time << endl;
cout << " Avg time in CPU = " << totalburst / intervals << endl;
cout << " Avg Quantum = " << Q << endl;
cout << " Average Burst = " << float (totalburst) / N << endl;
cout << " Total time = " << time << endl;
cout << " Idle time = " << idletime << endl;
outfile << " Scheduling type = " << stype << endl;
outfile << " Average wait time = " << avgwait << endl;
outfile << " Average arrival = " << avgatime << endl;
outfile << " Throughput = " << float (N) / time << endl;
outfile << " Avg time in CPU = " << totalburst / intervals << endl;
outfile << " Avg Quantum = " << Q << endl;
outfile << " Average Burst = " << float (totalburst) / N << endl;
outfile << " Total time = " << time << endl;
outfile << " Idle time = " << idletime << endl;
// cleanup follows
procfile.close ();
delete[] ready;
delete[] arrival;
}; // schedule()
void main ()
{
int N, // number of processes
K, // max burst
P, // max priority
M, // max arrival time
Q, // quantum
input = 0, // scheduling choice input
count = 0, // flag to repeat the loop
trial,
notdone = 0; // input flag
sched_type Schedule;
outfile.open("proj3.txt",ios::out);
randomize (); // tell Borland to actually be random this week
cout << endl << "Welcome to Ryan's (C) Process Scheduling System" << endl
<< " Copyright 1997 " << endl;
do{
cout << " Input some data for me: ";
cout << endl << "Processes: ";
cin >> N;
cout << " Burst: ";
cin >> K;
cout << " Priority: ";
cin >> P;
cout << " Arrival: ";
cin >> M;
cout << endl << " Choose a scheduling type " << endl;
cout << "0: FCFS" << endl << "1: SJF" << endl << "2: SJR"<<endl
<<"3: RR" << endl <<"4: Pr" << endl;
cin >> input;
switch(input)
{
case(0):Schedule = FCFS; break;
case(1):Schedule = SJF; break;
case(2):Schedule = SJR; break;
case(3):Schedule = RR; break;
case(4):Schedule = Pr; break;
};
cout << " Schedule = " << Schedule << endl;
cout << " How many times? " ;
cin >> count;
for(trial=0;trial<count;trial++)
schedule(N,Schedule,K,P,M);
cout << endl << endl << "Press 0 to stop, or 1 to continue: " ;
cin >> notdone;
}
while(notdone);
outfile.close();
};
// These functions were stolen from the source code I had left from CSC 220
// These have been hacked to be useful here, and should not be considered
// *ANYTHING* I am proud of to look at all. Please ignore this code, and
// assume it works. :-)
//************************************************************************
// Functions for mergeSort
template < class elementtype >
int precedes (const elementtype & x, const elementtype & y)
{
if (x < y)
return (-1);
else if (x == y)
return (0);
else
return (1);
}
template < class elementtype >
void swap
(elementtype & x, elementtype & y)
{
elementtype temp;
temp = x;
x = y;
y = temp;
}
//------------------------------------------------------------------
// Interface for function merge:
// GIVEN: Source array arranged in ascending order between indices
// lower..mid and mid+1..upper respectively.
// RETURN: Complete order list in destination array.
// TASK: Merge the two ordered segments of source into one list
// arranged in ascending order.
void merge (processM * source, processM * destination,
int lower, int mid, int upper, sfield field = atime)
{
int s1, s2, d; // Pointers into two source lists and destination
int less = 0;
// Initialize pointers
s1 = lower;
s2 = mid + 1;
d = lower;
// Repeat comparison of current item from each list.
do
{
switch (field)
{
case (atime):
less = (source[s1].atime <= source[s2].atime);
break;
case (burst):
less = (source[s1].burst <= source[s2].burst);
break;
case (priority):
less = (source[s1].priority <= source[s2].priority);
break;
case (pnum):
less = (source[s1].pnum <= source[s2].pnum);
break;
case (tleft):
less = (source[s1].tleft <= source[s2].tleft);
break;
case (seq):
less = (source[s1].seqnum <= source[s2].seqnum);
break;
default:
less = (source[s1].atime <= source[s2].atime);
break;
};
if (less)
{
destination[d] = source[s1];
s1++;
}
else
{
destination[d] = source[s2];
s2++;
}
d++;
}
while (s1 <= mid && s2 <= upper);
// Move what is left of remaining list.
if (s1 > mid)
{
do
{
destination[d] = source[s2];
s2++;
d++;
}
while (s2 <= upper);
}
else
{
do
{
destination[d] = source[s1];
s1++;
d++;
}
while (s1 <= mid);
}
} // of function merge
//------------------------------------------------------------------
// Interface for function order:
// GIVEN: Source and destination arrays that are initially identical
// between indices lower..upper.
// RETURN: Destination array arranged in order between indices
// lower..upper.
// TASK: Transfer source array values in ascending order to the
// destination array, between indices lower..upper.
void order (processM * source, processM * destination,
int lower, int upper, sfield field = atime)
{
int mid;
if (lower != upper)
{ // Recursively call to get smaller
// pieces which are then ordered.
mid = (lower + upper) / 2;
order (destination, source, lower, mid, field);
order (destination, source, mid + 1, upper, field);
merge (source, destination, lower, mid, upper, field);
}
} // of function order
//------------------------------------------------------------------
// Interface for function mergeSort:
// GIVEN: Array with entries in indices low..high.
// RETURN: Array arranged in ascending order between low..high.
// TASK: Apply merge sort algorithm.
void mergeSort (processM * Key, int low, int high, int size, sfield field = atime)
{
processM *CopyKey = new processM[size];
int k;
// Make copy for call to order.
for (k = low; k <= high; k++)
CopyKey[k] = Key[k];
order (CopyKey, Key, low, high, field);
} // of function mergeSort
Statistics for all Scheduling Types
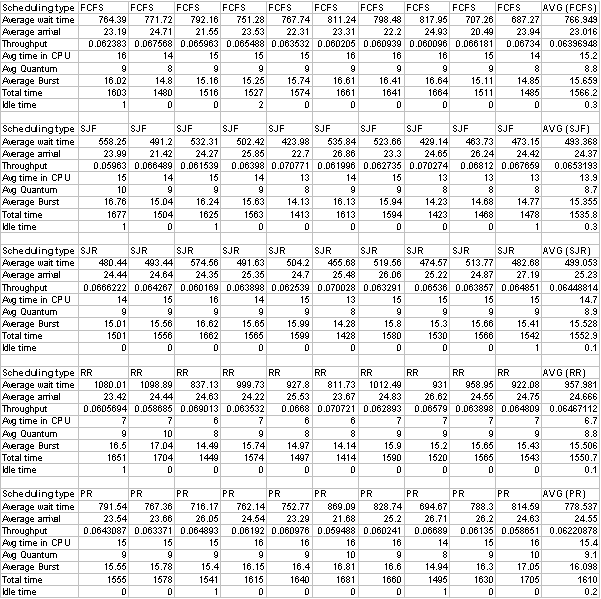
 Average wait time is defined by the sum for all processes of the last time a process got the CPU, minus it's
previous time in CPU, minus its arrival time, all divided by the number of processes. Average arrival is a simple
mean of the arrival times of all the processes. Average Throughput is number of processes over time. I chose this to
be number of processes over Time. (Time is the total time the processor spent executing a selection of processes).
The average time in CPU is calculated by the totalburst time of all processes divided by the number of intervals on
the Gantt chart. This is calculated in my algorithm as intervals and is incremented every time a change in process
occurs. The average quantum is calculated base on 60% of the average burst. On that note, average burst is
totalburst (defined above) over number or processes. Total time is the total time it took to execute all these
processes, including any idle time waiting for a new process to be ready. Typically, idle time only occurred at the
beginning of an execution, when no processes arrived at time 0, and in one case time 1. See the attached detailed
Excel tables for statistics on each simulation run.
Average wait time is defined by the sum for all processes of the last time a process got the CPU, minus it's
previous time in CPU, minus its arrival time, all divided by the number of processes. Average arrival is a simple
mean of the arrival times of all the processes. Average Throughput is number of processes over time. I chose this to
be number of processes over Time. (Time is the total time the processor spent executing a selection of processes).
The average time in CPU is calculated by the totalburst time of all processes divided by the number of intervals on
the Gantt chart. This is calculated in my algorithm as intervals and is incremented every time a change in process
occurs. The average quantum is calculated base on 60% of the average burst. On that note, average burst is
totalburst (defined above) over number or processes. Total time is the total time it took to execute all these
processes, including any idle time waiting for a new process to be ready. Typically, idle time only occurred at the
beginning of an execution, when no processes arrived at time 0, and in one case time 1. See the attached detailed
Excel tables for statistics on each simulation run.
